Şifreleme Bilimi ve Yöntemleri

Matematiği sevmeyenler için şifreleme bilimi ve yöntemleri

Öncelikle matematik dediğimizde çoğunlukla aklımıza formüller mi geliyor… Hep ezberlemeye alıştığımız ve korktuğumuz için böyle düşünüyoruz. Aslında matematik deyince sistematik bir durumun aktarılması gibi düşünmemiz gerekiyor. Bu konuda korkuyu sevgiye dönüştürmek için Sinan Canan’ın kaos ile ilgili yazılarını okumanızı öneririm. Matematiğin de basit bir dille anlatıldığında çoğu insanı etkilediğini görüyoruz. ( hatta Sinan Canan da geçmişte matematikten korkan birisi imiş)

Peki nedir bu şifre?

Dediğimiz zaman karşımıza neler çıkıyor: “kökeni sıfır’a dayanıyor”… 

Ama şu anda biz günlük dilde “şifreyi unuttun mu” derken, tabii ki kullanıcı doğrulaması yaparken kullandığımız şifreden bahsediyoruz.

Turk Dil Kurumu'na göre şifre kelimesi Türkçeye Fransızca chiffre kelimesinden girmiş. 

İngilizcedeki "cipher" kelimesinin kökeni eski Fransızca ciffre kelimesi. 

Ciffre kelimesinin kökeni ise arapça şifr kelimesi. 

Şifr kelimesi de aslında hepimiz bildiği Sıfır.  (1)

TDK

(şi'fre), Fransızca chiffre

1. isim Gizli haberleşmeye yarayan işaretlerin tümü; kod:
      "İstanbul mümessilliği şifresiyle Mustafa Kemal Paşa'ya, bekledikleri malumatı iletmiştim." - Yakup Kadri Karaosmanoğlu

2. isim Gizliliği olan kasa, kapı, çanta vb. şeylerin açılması için gereken rakam. (2)

Şifreleme diye Türkçe bir kavram kullanıyoruz, ancak burada yapılan mesajı gizlemek için yapılan hareketi tam anlatmadığını düşünüyorum. Bu kelimeyi kullandığımızda, kriptoloji kavramlarını sadece Türkçe’den okuyan kişiler için bir hayli karışık gelebilir. Bu da teknik konuları gittikçe  karıştırır.
Bir önceki yazımızda şifreleme algoritmalarının nasıl çalıştığını anlatmıştık. (3) Burada da aslında mesajı şifrelemek yerine kilitleme dememiz konuyu anla(t)mamız için gerekiyor.

kilitlemek

1.  Anahtarla kilidi kapamak:
      "Kapıyorum zannıyla kilitlemişim, diyordu." - Mithat Cemal Kuntay (4)

“Evin kapısını kilitledim”… bu hareketi yapmak için neye ihtiyacımız var: bir kilit sistemi ve anahtar. İşte gizlilik(confidentiality) sağlayan algoritmalar da bu şekilde çalışıyor: bir kilit(algoritma) ve anahtar(key).

“Google’a girerken https siteden giriyorum, kendimi güvende hissediyorum” diyor bir arkadaş. Burada hangi kilit sistemi kullanılıyor, hangi algoritmaları hangi anahtar ile kullanılıyor.  

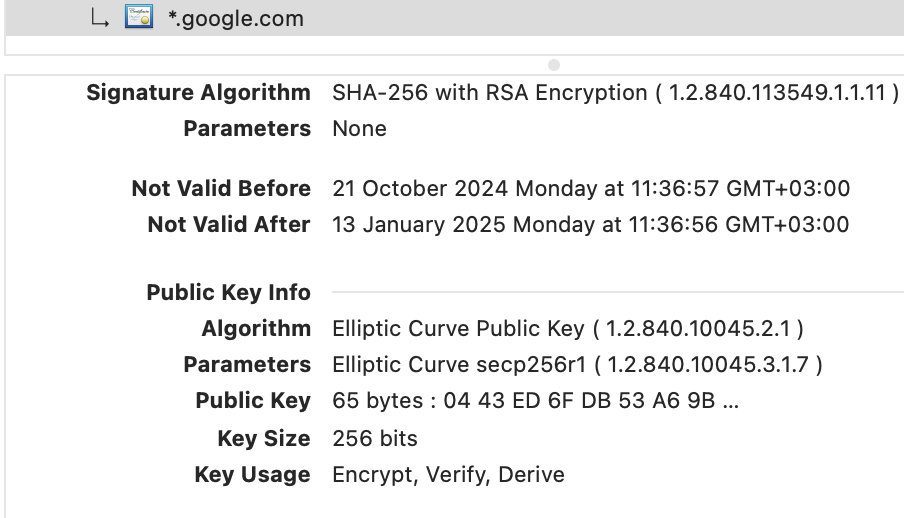
İlgili web sitesinin detayına girdiğimizde anahtar ve algoritma detayını da görüyoruz:

Bir anahtarımız var (Public Key) + bir de asimetrik anahtar kullanan algoritmamız var (Elliptic Curve). 

Bu anahtar asimetrik algoritma ve simetrik bir algoritma ile mesajlarımızı KİLİTleyip Google’a gönderiyoruz. Bu kadar basit (mi acaba? 🙂 )

Şifre Bilimi;

Kriptoloji diyince, Google’da nasıl bir tanım karşımıza çıkıyor:

“Kriptoloji, şifre bilimidir. Haberleşme ve iletişim alanında iletilerin, mesajların, yazıların güvenli şekilde alıcısına ulaşması için çalışmalar yapan, yöntemler geliştiren bilim dalıdır.”

Yani amacımız mesajlarımızın güvenli bir şekilde ulaşması ancak biz güvenli dediğimiz noktada kafamızda sadece gizlilik(confidentiality) beliriyor.  Aslında kriptolojide birçok farklı tipte matematiksel araçlar kullanıyoruz.

Kriptoloji ile siber güvenlik sağlamak için birçok araca sahibiz. Yani artık bir tamircinin el çantası gibi elimizde birçok alet var. Çantanın içine baktığımızda neler var?

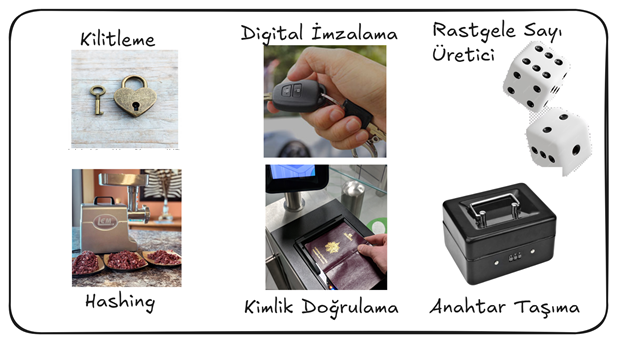
Kilitleme ve kilit açma (encryption-decryption) dan bahsetmiştik. İkinci olarak kıyma makinasını çantamızda taşırsak siber güvenlikte ne işimize yarayacak?

Hash fonksiyonları nasıl çalışır?

Haberleşme ve iletişimde bir de verinin değişmediğine de emin olmamız gerekiyor.

Yoksa banka transferi yaparken gönderdiğim para gizli(confidential, kilitli) olabilir ama başka biri bu veriyi değiştirirse, benim için zarar (veya şans eseri fayda) olacaktır. O zaman benim bir de verimin bütünlüğünü de koruyor olmam gerek. 

İşte burada da  matematik devreye giriyor. Örneğin bir mesajından içindeki  “ismimMehmet, TCKN:123113”  verisinin bütünlüğünü nasıl kontrol edebilirim…

Çok önemli olmayan bir veri olsaydı, mesaj açık ve kısa bir şekilde geldiğinde de, bazı kısımlarını kontrol edip değişmediğini kontrol edebilirdik. Ancak önemli veriler olduğunda bu bu mesaj için farklı önlemler alıyoruz, yani basit bir matematikle kontrol edebiliyoruz.

Annem beni biliyor ki, makarnayı kıymasız yiyemem… “Oğlum git bir kilo kıyma al gel…” Eti alan kasap kıyma makinasının girişine götürdü, çıkışta bir baktım küçük parçalara bölünmüş…  Kasap arkadaşa dedim ki, “vazgeçsem kıymadan, onu tekrarda ete dönüştürsek… “. Yok dedi olmaz öyle, bu veri geri dönmez… Dolayısıyla iyi bir “hash” fonksiyonu aynı zamanda geri döndürülemez (irreversible) özellikte de olmalı.

hash (v.) 

1650s, "to hack, chop into small pieces," from French hacher "chop up" (14c.)

Bir veriyi küçük bir parçaya çevirdik ve bunu da matematiksel bir fonksiyon (hash) kullanarak yaptık. Sonrasında da tek gereken, mesajı alan kişinin de veriyi aynı makinaya sokup aynı kıymayı alması. Sonra da diyecek, evet benim gönderdiğim mesajın özeti de buydu…Bu kadar basit (mi acaba? 🙂)

İşte birçok verimizin bütünlüğünü için kullandığımız SHA, MD5 gibi fonksiyon(algoritmalar) da temelde bu şekilde çalışıyor. Peki burada matematiği nasıl kullanıyoruz? Kullandığımız tüm mesajların dijital dünyada 1 ve 0’lara denk geldiğini biliyoruz. 

Mesajımızı en basit bir şekilde HASH’lemek için bir XOR fonksiyonu kullanabiliriz. XOR fonksiyonu ne yapar? İki girdi arasındaki matematiksel olarak fark varsa,  1 sonucunu verir. (Aynı ise 0 döner) Dolayısıyla mesajımızı öyle bir duruma getirir ki, o mesajı inceleyen kişi verimizi anlayamasın. 

Ancak XOR gibi basit fonksiyonlar, iyi bir “hash”ing (SHA, MD5 VB.) fonksiyonlarının sağladığı, geri döndürülememe ve aynı çıktı oluşturmama (collision resistance) yeteneklerine sahip değildir. (6)

(örnek bir XOR fonksiyon ile verimizi özetleme/hash’ing)

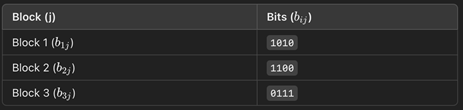
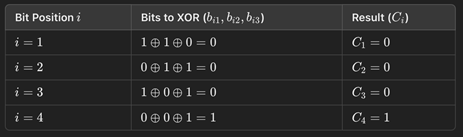
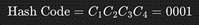
Gelişmiş bir matematiksel fonksiyon örneği için kitabına ve bu resime bakabilirsiniz. (7)

O veri, benim verim

“O mektup benim, yemin ederim bak…” bu mesaj eskiden verinin bizim olduğunu kanıtlardı ama şu an değil. 

“Bak bu kağıdın şurasına imza da atmışım…” Bu mesaj eskiden verimizin bizim olduğunu kanıtlardı ama şu an değil.

“Bak bu mesajımı dijital imzalayarak gönderiyorum…” bu veri kesin benim verim, Evet (mi acaba? 🙂 )

Dolayısıyla o verinin benim verim olduğunu (dijital) imzalamalarla kanıtlıyoruz, evet imzalatıyoruz… 

Dijital imzalama için ne gerekiyor?

Yine bir kilit ve anahtar. Kilit yine matematiksel fonksiyonlar-algoritmalar olarak düşünürsek, peki elimizdeki anahtar ile kilitleyince onun benim verim olduğunu nasıl anlıyorlar?

*private key*

Çünkü aynı kilitten başkalarında da olabilirdi… O anahtara/kaşeye eğer güven varsa veya o anahtar dünyada bir tek sizde varsa…bu sefer işler değişiyor. Karşı taraf da diyor ki evet, bu mesaj Mehmet Ali’nin… (mi acaba? 🙂 )

İşte bu yüzden önemli olan neydi, anahtarı kaybetmemek/düşürmemek… Düşürürsek, eve giremeyiz, işe gidemeyiz… Sonra da ne olur, (internette) gezinemeyiz. Güvensiz hissettiğimiz yerlerde oluruz. Ama bunun çözümü basit,  anahtarı yanımızdan ayırmayız, onu saklarız veya üstünü sararız.

Peki bu anahtarlar hep bizde mi durur, eve giren başka kişi de olmaz mı?

Anahtar Yönetim süreçleri (Key Management)

İstanbul’da eve yeni taşındık, annem dedi: “Ben ayın 15’inde gelecegim, sen evde olmasan bile ben de eve girebileyim”.

Nasıl olacak bu iş (anne)? Tek anahtarımız var ve ben de ayın 15’inde Ankara’ya gidecektim. Düşündüm, sonra dedim ki bu anahtarı ben kopyalatayım, bir tanesini de anneme göndereyim.

Çilingir abimize gittim, o kopyaladı. Anahtarı kargoya verdim, çalındı. Şimdi ne olacak? 

Onu öyle bir forma sokup göndermeliyim ki, kargocu paketimi alsa bile anahtarımı çalamasın. (Sayısal) anahtarıma bir güzel paket yapacağım. 

Hem de büyük bir gösteriş olacak. (Big number exponent) . 

(Anahtar taşıma paketim)

İşin matemağine baktığımızda, paketimin içine 5 koyuyorum, mesajım bu oldu.

5’i n (6) (mod 2027) alarak kilitliyorum,

Bu aritmetik operasyonu sayesinde karşı taraf mesajımı 1436 olarak alıyor.

(Kargo paketim)

Buradaki matematik temel anlamda şu şekilde işliyor:

• Biz bir sayının üssünü almayı biliyoruz, 5^2  = 25 diyebiliyoruz,
• Aynı şekilde bir sayının bir bölene karşılık kalanı da bulabiliyoruz, yani modunu alabiliyoruz. 
  25 (mod 17) ) = 8  veya 25/17 böldüğümüzde kalan 8’dir.
• Peki burada ifadedeki x’i bulmamız kolay olur mu?
  5^x = 5 mod 17

Evet, küçük sayılarda bulmamız kolay. Matematikte burada sorunu çözmek için logaritma devreye giriyor. Kavram kafamızı karıştırmasın, çünkü logarithm bize buradaki üstteki x sayısını bulmamıza yardımcı olur. Her iki tarafı da logarithm içine alırsak, log5 bazında x kolay bir şekilde bulabiliyoruz.

x=log5 ​(5 (mod 17)) dönüşüyor, bu da x’in 1 eşit oldugunu buluyoruz.

diğer bir örnekte ise küçük sayılarda hemen kafamızdan bile logaritma alıp n=3 diyebiliyoruz:

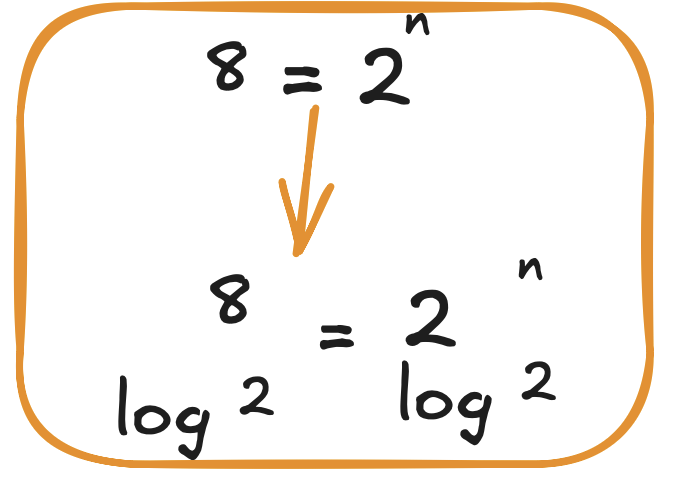
Peki diyelim ki buradaki sayıyı büyük rakamlara çevirsek, buradaki n bulmak imkansız hale gelebiliyor.
Tabii ki bu olayı matematikçiler keşfediyor ve anahtarlarımızın dağıtımında kullanıyorlar.

Diffie-Hellman Key exchange protokolü:

Şimdi işleri kargocular ve hırsızlar için biraz daha zorlaştıralım, büyük rakamlar ve asal sayıları denklemlerimize sokacağız

Logarithm Discrete Problem:

İşte matematikçiler(aşagıda ilgili protokolü ismin geldiği Diffie ve Hellman’ın fotoğrafları da var) demiş ki, kolaysa bunu çözsünler(kargocular, hırsızlar vb.)...

Şimdi diyelim ki 2 diye bir mesajımız var ama karşı tarafa 9 olarak ulaştırıyoruz.

(Aradaki kargocu abimiz de bu mesajı üssel sayı ile süslediğimizi ve hangi sayıya böldüğümüzü ( modulo operasyonu) biliyor. 

Buradaki kargocu abi, kargoyu nasıl kilitlediğimizi kolay bir şekilde buluyor. 

Önce n=1 dener, sonra 2,3.. derken 6 olarak bulabilir.

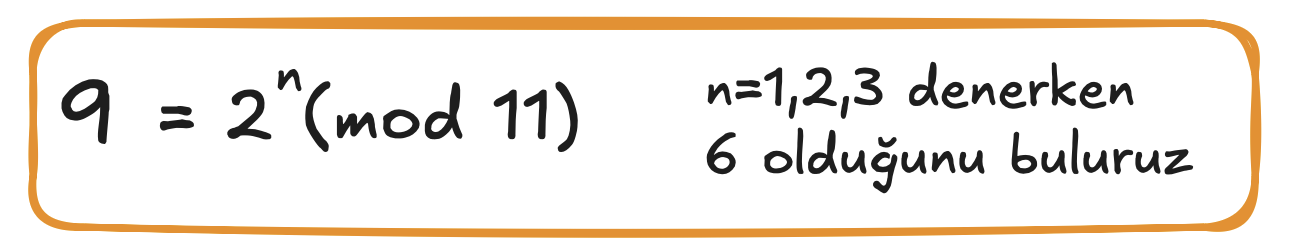
n’i bulunduğunda, artık anahtarı kargocuya vermiş durumdayız. Çünkü bu algoritmadaki mod x sayısı ,sonucunda çıkan 9 sayısını verirsek ve ilk denemelerinden sonra benim mesajımı da tahmin edebiliyor.

Ne demiştik?  “İşte bu yüzden önemli olan neydi, anahtarı kaybetmemek/düşürmemek… “

Artık mesajlarında kargocu göndericinin hangi özel sayı ile mesajını gizlediğini bulup, sinsi bir şekilde bu mesajları çözebilir.

Ama sayılar büyüdükçe buradaki matematiksel problem, çok zorlaşıyor. Dolayısıyla da veriyi gören kişi de çözemiyor.

(p’yi örnek olarak 78 haneli büyük bir sayı seçtiğimizde)

Paket çözülmeyince, biz de rahat rahat anahtarlarımızın dağıtımını yapıyoruz, hem de bedava…

Ama kargocular ya kötü niyetli ise.. kargoyu açmayı denemek yerine şunu da yapabilir. Aldığı kargo paketini kendi özel hazırladıkları paket ile değiştiriyorsa…

O zaman bir de gelin, krigtografik doğrulama önlemine bakalım.

Kimlik doğrulama (Authentication) nedir?

Kimlik doğrulama. Pasaport kuyruğuna girdim, elimde pasaportum var. Görevli bir bana bakıyor, bir de pasaportuma… Yüzüme bakıp, bir de pasaport fotoğrafıma bakıyor… Önemli bir fark görmezse geç diyor… Kimliğim doğrulandı.

İşte internette de böyle yapıyoruz: En basit kimliğimiz ne: Kullanıcı adımız, ID’lerimiz vb.

En basit doğrulama yöntemimiz: Parolalarımız...

Dolayısıyla matematik çok basit, doğru parolayı girsem, sistem de bu benim girdiğim parola ile karşılaştırıyor. Formüle gerek yok.

Tabii ki, çoğu durumda kimliğimizi doğrulamamız için sadece parolamız yetmiyor. Ek bir doğrulama olarak da bir kerelik oluşturulan “password” ekliyoruz.

Çok Faktörlü Kimlik Doğrulama (Multi Factor Authentication) ile doğrulama nedir?

Hiçbir sistem %100 güvenli değildir, ama tek faktörlü doğrulama sistemlerinin zayıf bir koruma sağladığını biliyoruz. O zaman ikinci bir faktörü devreye sokuyoruz. Diyelim ki OTP (one time password) doğrulaması da gerekiyor.

Bu sefer sistem ne yapıyor, parolanız ile birlikte ürettiği OTP’yi, sizin girdiğiniz verilerle karşılaştırıyor.

Kullanıcı: Mehmet Parola: Mehmeteor OTP: 124367 

Verisi ile sistemdeki veri karşılaşıyor. (Tabii en basit haliyle bu şekilde anlatabiliriz)

Burada nerede matematik var?

Diyebiliriz, öyle bir matematik yapmalıyız ki, tahmin edilemeyecek şekilde rastgele 6 rakam versin. Buradaki rakamların matematik ile nasıl üretildiğini de sizin araştırmanıza bırakıyorum…

(Çok basit rastgele sayı üretici)

Dolayısıyla bir matematik bilimi nelere kadirmiş, matematik sayesinde de daha güvendeyiz, en azından sanal dünyada… Matematiği biraz daha sevdirin, yayalım bu bilgiyi…ve bu detaylar ile kafamız karışmadan konu bizde kalsın 😊 Güvenli internet gezinmeleri…

https://tr.linkedin.com/pulse/%C5%9Fifre-kelimesinin-nereden-geldi%C4%9Fini-biliyor-musunuz-buyukkahraman
https://sozluk.gov.tr/
https://gelecegiyazanlar.turkcell.com.tr/blog/simetrik-ve-asimetrik-sifreleme-algoritmalari
https://sozluk.gov.tr/
https://www.sciencedirect.com/topics/computer-science/asymmetric-cryptography